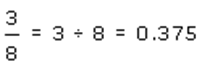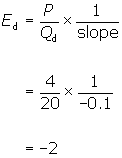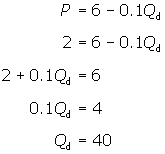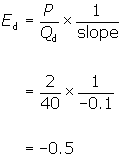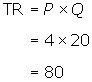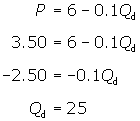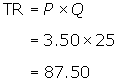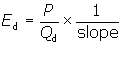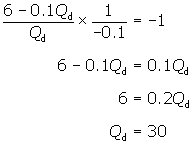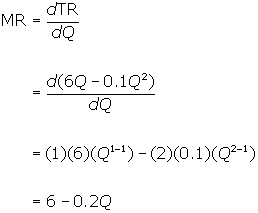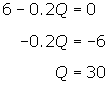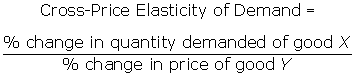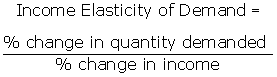3.3
Price Elasticity
[3.2 Demand]
[3.4 Supply]
[3.5 Production] [3.6 Costs]
Why is it that members of the Organisation of Petroleum
Exporting Countries (OPEC) can increase their total revenue by selling less
oil? The answer is, by selling less oil, they can drive up its price on the
world market. The world's oil consumers may decrease their consumption of oil
in response to the price increase, but the decrease in consumption is fairly
small. In fact, it’s small enough that the increase in price more than offsets
the decrease in quantity sold. The total revenue that oil producers receive
rises as a result, as does the motivation of producers to restrict the output
of oil.
The
OPEC example illustrates a fundamental concept in economics known as elasticity. Elasticity measures the
relative response in one variable to a change in another variable. For example,
the price elasticity of demand for oil
measures the relative response in the quantity demanded of oil to a change in
the price of oil.
Similarly,
the price elasticity of supply of tomatoes
measures the relative response in the quantity supplied of tomatoes to a change in the
price of tomatoes. The cross price elasticity of demand of
coffee with respect to tea measures the relative response in the quantity
demanded of coffee to a change in the price of tea. The income elasticity of demand of housing
measures the relative response in the quantity demanded of housing to a change
in consumer income.
Click here to take a look
at the impact of elasticity on America Online.
Now view the following animation to find out more about
price elasticity.
Price
Elasticity of Demand
Firms
in competitive markets like to know the price elasticity of demand for their
products because it helps them to determine what prices will maximise profits.
Price elasticity of demand is closely related to a firm's total revenue and
marginal revenue from selling a product. Its importance in the price-setting
process and, therefore, cannot be overstated. However, since firms in competitive
markets typically have no control over the price of their products, this
information may be of limited use to them.
Formally, the price elasticity of demand measures the
percentage change in the quantity demanded (Qd) of a
good, X, relative to the percentage change in the price (P) of good X.
The formula for price elasticity of demand is
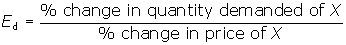
Elasticity
is derived as a fraction. To review fractions, click on the link below.
Analytical Methods: Fractions
A percentage change can be calculated as the "change in"
a variable divided by its starting value. Therefore, you can write the price
elasticity of demand (Ed)
as

For a linear demand curve such as
P = a - bQd
the slope parameter -b gives you

Therefore, for the elasticity
calculation, you need to invert the slope to find

The Inverse of the Slope
You can then calculate the price
elasticity at any point along a linear demand curve by applying the point-slope
formula.
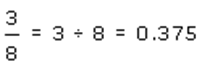
slope =
the value -b from the demand equation

Sometimes you have a set of
price/quantity combinations for which you want to calculate elasticity. For
instance, suppose that you are given the following demand information for sales
of a music CD and would like to calculate the price elasticity of demand at $12.
|
Price
|
Quantity
(Sales per Month)
|
|
$11
|
1,100
|
|
$12
|
1,000
|
|
$13
|
925
|
You decide to do this by examining the
effects of a price change from $12 to $13. It will help to solve this if you
rewrite the formula for elasticity in the following way:

Q0 and P0
represent the starting price and quantity (in this example, $12), while Q1 and P1 represent the ending
price and quantity (in this example, $13). To find the elasticity, simply
insert the demand information given.

You may be wondering if the calculation
of elasticity at $12 would change if it were calculated instead by examining a
price increase from $11 to $12. The answer is yes. To see this, recalculate
elasticity using the formula above.

Click here to see two examples of how to
calculate elasticity using demand information.
Price
elasticity of demand using the point-slope formula
Another method of
calculating elasticity is using the point-slope formula. Suppose a coffee shop
faces the following linear daily demand curve for cups of coffee:

What is the price elasticity of demand
at a price of $4 per cup?
At a price
of $4, consumers would want to buy 20 cups of coffee per day.

Using P = $4, Qd
= 20, and slope = -0.1, the price elasticity of demand is
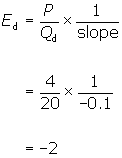
Note that it is also common to see
price elasticity reported as an absolute value. Here, at a price of $4, Ed = 2.
Elasticity
along a linear demand curve
The
coffee shop example allows for the demonstration of another important point.
The value of elasticity of demand typically varies along a demand curve. In
fact, it will always vary along a linear
demand curve.
For
example, calculate the price elasticity of demand for coffee at the coffee shop
at a price of $2 per cup. When P = $2,.03 the demand function yields quantity demanded of 40
cups.
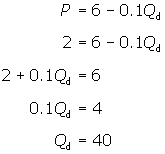
The slope of the demand curve is still
-0.1, so price elasticity of demand is
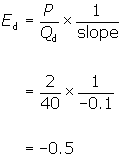
Notice that demand is more inelastic
(that is, Ed is smaller in
absolute value) at the lower price of $2 than at $4. It may seem odd that the
elasticity of demand differs at prices of $2 and $4, when the slope of this
demand curve is the same at all points. This fact can be explained by
considering the percentage changes in
price and quantity in each case, rather than the absolute changes.
Because the slope of the demand curve
in the coffee shop example is -0.1, a one-unit increase in quantity demanded
will occur for each $0.10 decrease in price. Notice that if the quantity
demanded is 20, an increase in quantity of one unit is a 5 percent change in
quantity demanded.
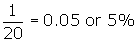
At a price equal to $4 (which
corresponds to a quantity demanded of 20), a $0.10 decrease in price is a -2.5
percent change in price.
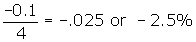
Therefore, the price elasticity of
demand, defined as the percentage change in quantity demanded divided by the
percentage change in price is -2.

However, when quantity demanded is 40,
a one-unit change is only a 2.5 percent change, which is smaller than the 5
percent change calculated above.
Because quantity is already large, a
one-unit increase is not as significant. On the other hand, a price change of
$0.10, when the price is only $2, is a 5 percent change.

Because the price is starting out low,
this $0.10 change is more significant in percentage terms. The price elasticity
of demand when P = $2 and Qd =
40 is -0.5, as you saw before.
Even though the absolute changes in price and quantity are the same in these two
examples, the percentage changes are
quite different.
Understanding percentage changes and elasticity
will help you answer questions such as: Is a $0.10 price increase significant?
The answer is, it depends. If the product sells for
thousands of dollars (a car, for instance), then an extra dime would go
unnoticed. If the product is a first-class postage stamp that sells for around
$0.35, an increase of a dime seems extreme. Similarly, an increase in quantity
demanded of 100 sandwiches would be insignificant to a fast-food chain that
sells millions of sandwiches, but the same increase would be meaningful to a
local sandwich shop that may sell only 500 sandwiches a week.
To review why elasticity differs along
a linear demand curve, take a look at the following animation.
As you will soon see, the ratio of the
percentage change in quantity demanded to the percentage change in price (the
price elasticity of demand) is important for determining how the total revenue
of firms will change in response to changes in price or quantity.

Before making the connection between
total revenue and price elasticity of demand, you will learn some terminology
that economists use to classify elasticity conditions. You will see later that
these classifications help summarise how changes in price will affect total
revenue.
The numerical price elasticity of demand
must fall between zero and negative infinity. You can classify the sensitivity
of quantity demanded to price changes according to the value of the price
elasticity of demand. To motivate the categories you will use, first consider
three special cases of demand curves. These demand curves correspond to
perfectly inelastic, unit elastic and perfectly elastic demand.
Click here to consider perfectly inelastic demand.
Click here to consider unit elastic demand.
Click here to consider perfectly elastic demand.
The
cases of perfectly inelastic and perfectly elastic demand are extreme examples.
Price changes cause either no change in quantity demanded or infinite changes.
When the demand curve is unit elastic, price and quantity demanded change by
the same percentage (though in different directions).
Inelastic
demand
In general, economists say that demand is inelastic over any price range
where

This relationship is
expressed as an inequality. To review the mathematics of inequalities, click here.
Quantity
demanded is relatively insensitive to price changes. A 5 percent increase in
the price of a good causes quantity demanded to fall
by less than 5 percent.
Demand for Table Salt
Elastic demand
Similarly, demand is said to be elastic if

When demand is elastic, quantity
demanded is relatively sensitive to price changes. A 5 percent increase in the
price of a good causes quantity demanded to fall by
more than 5 percent.
In the coffee example above, the demand
for coffee is elastic (Ed)
at a price of $4 per cup. The price elasticity of demand can help answer the
following questions: Is it optimal for the firm to charge $4 per cup? If not,
should the firm charge a higher or lower price? What is the relation between a
firm's total revenue and marginal revenue from the sale of its product and the
price elasticity of demand for the product?
Wondering what elasticities occur
in the real world? Take a look at the following here.
Click on each of the following links to view
characteristics that influence the price elasticity of demand for a good or
service.
Availability of Substitutes
A Product's Cost as a
Percent of the Buyer's Budget
Price Elasticity of Demand, Total Revenue and Marginal Revenue

Knowing the price elasticity of demand
for a product alone does not, in general, provide sufficient information to
determine the optimal price a firm should charge. A firm must also consider its
costs of producing the good. However, because of the relation between price
elasticity of demand and total revenue, knowing the price elasticity does
provide useful information for price-setting decisions.
To see why, start by considering a
firm's total revenue. For a firm that charges all consumers the same price for
its product, the firm's total revenue equals the price (P) it charges t the number of units (Q) it sells. That is,
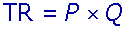
A firm's marginal revenue measures the
change in its total revenue from selling an additional unit of its product. To
find marginal revenue, take the derivative of total revenue with respect to
quantity Q. That is,

This
is expressed as the derivative of total revenue with respect to quantity. For a
review of derivatives, click on the following link.
Analytical Methods: Derivatives
For perfectly
competitive firms that often have no control over the price they can charge
(that is, they must simply accept the existing market price), marginal revenue
is constant and equal to the market price. The additional revenue a firm earns
by increasing the quantity it produces by one unit (marginal revenue) is simply
the market price.
Firms in competitive markets, then,
must decide only how many units to produce and sell. (See Topic 4.4 for more
information.) Note, however, that many producers acting together can influence
the market price even in competitive markets.
The OPEC illustration described earlier
provides one such example. Understanding the relation between the price
elasticity of demand and total producer revenue helps OPEC determine the
quantity of oil that each of its member countries should produce in order to
maximise total OPEC revenue.
A firm that has some degree of market
power (that is, a firm that can choose the price of its product) must consider
both the price to charge and the number of units to sell. (You can also see
Topic 4.2 for more information.) This is where price elasticity of demand
becomes important, as it determines the optimal markup
over cost a firm can charge to maximise its profits.
The
key is to understand what happens to a firm's total revenue if price is changed
by a small amount. The example below should help clarify this concept.
Example: Price Elasticity of Demand and Total Revenue
Suppose
the coffee shop in the example above lowers the price of a cup of coffee by a
small amount (from, say, $4 per cup to $3.50 per cup). What would you expect to
happen to the firm's total revenue from its coffee sales?
The
linear demand curve used in the coffee shop example is

Consumers would purchase 20 cups of
coffee at $4 per cup.

Therefore, total revenue would be
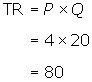
If the shop decreased its price to
$3.50 per cup, quantity demanded would increase to 25 cups per day.
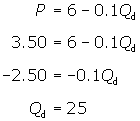
Therefore, total revenue would be
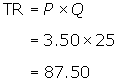
In this case, the firm's total revenue
from coffee sales increased when it decreased the price of its coffee. There
are two opposing effects on total revenue when there is a decrease in price.
The first effect comes from the firm charging a lower price on each unit it
sells. This first effect decreases total revenue. However, we know from the law
of demand that as price falls, the quantity of a good that consumers will be
willing to purchase rises. This second effect of a price decrease tends to
increase total revenue because quantity sold increases.
The net effect of a price decrease on
total revenue depends on what effect dominates, which is exactly what the price elasticity of demand tells us. The
fact that total revenue increased when price decreased from $4 to $3.50 is
consistent with the fact that demand was found to be elastic at a price of $4.
For an elastic demand, the percentage change in quantity demanded is larger
than the percentage change in price.
To summarise:
·
If demand
is elastic at the current price, then
total revenue will increase (implying positive marginal revenue of output) when
price is decreased. The additional revenue generated by increasing quantity
will be positive. This means that the percent change in price will be smaller
than the percent change in quantity demanded, causing total revenue to
increase.
·
If demand
is unit elastic, then total revenue
will not change. The additional
revenue generated by increasing quantity is zero. Thus, price and quantity
demanded change by the same percent, leaving total revenue unchanged.
-
If demand for the product is inelastic
at the current price, then total revenue will decrease (implying negative marginal revenue of output) when
the price is decreased. The additional revenue generated by increasing
quantity will be negative. This means that the percent change in price
will be larger than the percent change in quantity demanded, causing total
revenue to decrease.
The implications of this analysis for a
firm's price-setting decision are important. In general, a firm with some
market power will not maximise profits by setting a price at which demand is
inelastic. When demand is inelastic, a firm could increase revenue and decrease costs (because it sells
fewer units) by raising price.
This is because the percentage change
in quantity sold increases but the percentage change in price decreases, as one
moves upwards along the demand curve towards higher prices.
The logical conclusion of the analysis
thus far is that, for a linear demand, the price that will maximise a firm's
total revenue will be the price at which demand is unit elastic. The following
example illustrates this result.
Example:
Revenue-maximising prices and price elasticity
For consistency, return to the coffee shop example, where daily
demand for cups of coffee is given by

What price per cup should the coffee
shop charge to maximise total revenue?
Because a firm's total revenue is
maximised where demand is unit elastic, you need to find the unit elastic price
and quantity combination for this linear demand curve. To find the
price-quantity pair, begin with the point-slope formula for price elasticity of
demand.
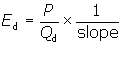
Set the elasticity equal to -1 and
substitute the appropriate slope and expression for price (taken from the
demand function).

Then solve for Qd.
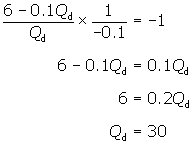
The result indicates that demand is
unit elastic at a quantity of 30 cups. To find the corresponding price,
substitute the value for Qd
into the demand function.

The demand for coffee at the shop is
unit elastic at a price of $3, which corresponds to a quantity sold of 30 cups
per day. Therefore, a price of $3 maximises total daily revenue. Total daily
revenue would be $90.

It is also true that the firm's
marginal revenue is zero at Q = 30
units, which you can demonstrate using calculus.
A firm's total revenue is price times quantity. From the demand function, you know the
relation between price and the number of cups that will be sold.
Therefore,

The firm's marginal revenue is the
derivative of total revenue with respect to quantity.
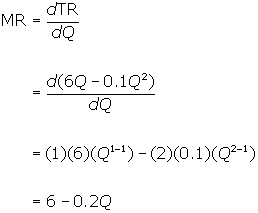
Notice that if you set marginal revenue
equal to zero and solve for Q, you
find that Q = 30.
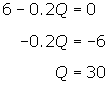
Marginal revenue is positive for all
units up to 30 and is negative for all units after 30. The graph below illustrates
this result. Notice that at 30 units of output, where demand is unit elastic, P = $3 and total revenue is maximised at
$90.

Does this mean that firms should set
price where demand is unit elastic? Again, the answer is generally no. Firms
are interested in maximising profits,
not total revenue. The only time the
two will coincide is when it costs the firm nothing to produce additional units
of its product (that is, when the firm's marginal cost of output is zero).
Test your knowledge now by evaluating a
proposal by a wildlife-conservation organisation to increase the price of its
T-shirts in order to increase total revenue.
Exercise: Wildlife Conservation Organisation
For additional information on
profit-maximising with positive marginal costs, see Topic 4.3.
What determines the price elasticity of
demand for a good? In short, goods that are necessities, have few good
substitutes, and/or constitute a small portion of a consumer's budget tend to
have more inelastic demand than goods that are luxuries, have many good
substitutes, and/or constitute a large portion of a consumer's budget. Also,
the longer the time period consumers have to react to price changes, the more
elastic demand will be. For example, if the price of petrol doubled overnight,
few households and businesses would respond with any significant decrease in
petrol consumption in the very short term. Over time, however, consumers would
find alternative ways to decrease petrol consumption (such as moving closer to
work, carpooling, taking public transportation, or purchasing more
fuel-efficient cars). This implies more elastic demand and a greater response
in quantity demanded to a price change over time.
The
following is a link to an advanced topic regarding demand curves where
elasticity remains the same over the entire curve.
(Advanced): Constant Elasticity (or Isoelastic) Demand Curves
Cross-Price Elasticity and Income Elasticity of Demand

A cross-price elasticity of demand
measures the relative change in the quantity demanded of one good in response to
a change in the price of a related good. Formally,
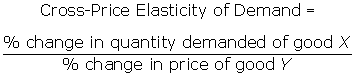
You can apply the cross-price
elasticity of demand to market demand for a good or to individual demand for a
good. For example, if the price of tea increases by 10 percent, causing the
total quantity demanded of coffee to increase by 20 percent, then the
cross-price elasticity of demand for coffee with respect to tea would be 2 (that
is, 20/10 = 2).
Notice that tea and coffee are
substitute goods for most people. Substitute goods will have
a positive cross-price elasticity, because an increase in the price of
one causes an increase in the quantity demanded of the other, as individuals
substitute away from the good whose price has increased.
On the other hand, two complement
goods, such as bread and butter, should have negative cross-price
elasticities. That is, an increase in the price of
bread will lead not only to a decrease in the quantity demanded of bread but
also to a decrease in the quantity demanded of its complement, butter. Two goods
that are unrelated should have cross-price elasticities
equal to zero.
Leisure airline fares are sometimes
accompanied by the reservation of a rental car. Recently, because of increases
in new-car prices, car rental companies have increased their prices by 5
percent.
For some people planning vacations,
this increase in rental car prices might persuade them to rethink their plans.
Instead of flying to their destination they might decide to drive there instead,
eliminating the need to rent a car.
Assume that there is a 3 percent
decrease in leisure fare purchases attributable to the increase in rental car
rates. With this information, calculate the cross-price elasticity of the price
change in rental cars and demand for leisure fares.

Because this cross-price elasticity is
negative, you can infer that the goods or services being measured are
complements. If the cross-price elasticity was positive, they would be
substitutes.
The
income elasticity of demand
measures the relative response in the quantity demanded of a good to a change in
consumer income. Formally,
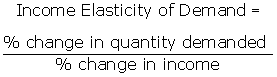
You can apply income elasticity of
demand to market demand or individual demand for a good.
For example, if your income increases
by 50 percent and you go to see 25 percent more movies, then the income
elasticity of your demand for movies is 0.5 (that is, 25/50 = 0.5).
For some goods, you might have a
negative income elasticity of demand. For example, if your income increases by
50 percent and your consumption of fast-food hamburgers decreases by 10 percent,
then your income elasticity of demand for fast-food hamburgers is -0.2 (that is,
-10/50 = -0.2).
Goods that have positive income
elasticities of demand are referred to in economics
as
normal goods. Goods
that have negative income elasticities of demand are
referred to as
inferior goods.
Click on each of the following links
for some more cases of applying elasticity
St. Louis
Philip Morris
Airline Travel
Click
here to run
through a guided practice.
Topic Summary
In this topic, you have learnt how to
·
calculate elasticity using
demand pricing data
·
identify factors that may make
demand more or less price elastic
·
use elasticity to understand
the sensitivity of quantity demanded to price and how total revenue changes
with price
·
apply elasticity to income and
cross price variables
Now go on to topic 3.4, “Supply”.
![]()